二進位

傳統上，電腦在傳輸訊息都是使用二進位，而二進位在加法與乘法有以下特性；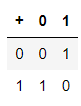


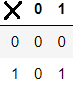
也就是說1+1=0，1+0=1，1x1=1。
在線性代數上，這樣的二進位字元被標記為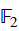

假設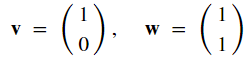


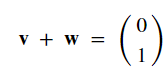
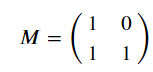
然後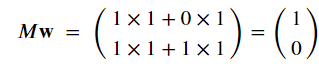

而在二進位上建立的m個維度的向量稱為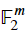
以下程式碼可以用來練習上面的內容

import numpy as np

print('(1 + 1) % 2 = ', (1 + 1) % 2)
print('')

# declare your vectors and matrices as numpy.array
# with a data-type of int, rather than the default
# type of float
M = np.array([[1, 0], [1,1]], dtype=int)
v = np.array([1, 1], dtype=int)
print('M = \n', M)
print('')

# if you add things as
print('M + M =\n', M+M, 'incorrect! 2 is not part of our number system.')
# you will get the wrong answer. '2' is not part of our number system.

print('')
# Instead mod everything 2. This is done with '% 2' in python
print('(M + M) % 2 =\n', (M+M) % 2, 'correct')
# The parenthesis in (M+M) % 2 are important

print('')
print('v = ', v)
# Remember that in numpy matrix multiplication is done using the @ symbol
print('M@v = ', M@v, 'incorrect')
print('M@v % 2 = ', M@v % 2, 'correct')

Classical linear codes

根據之前的有噪音版本的通訊圖來說，通訊過程的資訊都是以位元串的形式呈現，因此可以視為基於二進位的向量場

訊息空間

第一個向量欄位是包含訊息的向量欄位。對於我們將要研究的代碼類型，訊息的長度是一個固定的數字，我們將其表示為 𝑘 。如果要傳送的訊息較長，我們會將其分成長度塊 𝑘 ，然後將每個區塊視為自己的獨立訊息。在重複程式碼範例中，區塊的大小為 1

並且我們有以下定義

需要保護的資訊是一個長度為位元的字串 𝑘 ，每個這樣的字串稱為一條訊息。
訊息空間是向量空間 可能的消息。此向量空間表示為

程式碼空間

與重複碼一樣，對於線性碼，每個訊息在傳輸之前都會轉換為更長的位元串。這個較長的位元串稱為碼字，從訊息到碼字(codeword)的轉換稱為對訊息進行編碼。

訊息被轉換或編碼為碼字，碼字是長度為位的字串 𝑛

碼字有長度 𝑛 。有 長度的字串 𝑛 ，但只有 有效碼字 - 每個可能的訊息都有一個。因此，這裡有兩個向量空間。

程式碼空間是一個 𝑛 維向量空間，標記 。我們要求 𝑛≥𝑘

代碼空間通常不帶空格。對於重複碼，碼空間由所有長度組成 𝑛 = 3 位元串
{000,001,010,011,100,101,110,111}.
第二個向量空間是實際包含有效碼字的碼空間的子空間。對於重複碼，這是兩個碼字 {000,111}

代碼C 是一個 𝑘維子空間 。緊湊地，我們可以寫

因此，程式碼只是有效代碼字所在的向量空間的名稱。三個空間的關係如下圖所示。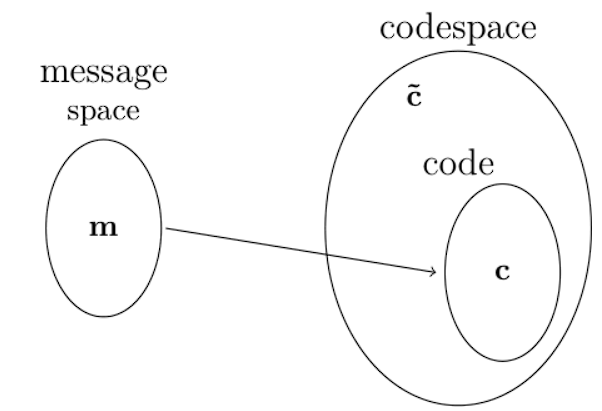

參考資料:https://github.com/abdullahkhalids/qecft